PyRamPL - Python Random Access Machine Simulation

• Link to the the Google Colaboratory notebook

  • The Google Colaboratory notebook has the advantage that you can run PyRamPl code from it without having to install PyRamPL or even Python on your local system.
  • You first need to copy it to your google drive
  • You can also download it to your local device and open it as a Jupyter notebook (if you have it installed with your Python).

Installing the PyRamPL package

• The PyRamPL package can be installed on your local system by running the following command from the command line

  pip install pyrampl

• Or you may try running one of the following commands from this notebook.
• If you are running it from a Jupyter notebook on your local system, then it will be installed on your device.

# To install from this notebook, run this cell.
%pip install pyrampl
# This should also work:
#!pip install --upgrade pyrampl

# After installation, you have to restart this notebook.
# Make sure to comment the %pip or !pip lines above to avoid reinstall each time you run this notebook.

# To uninstall the package use:
#%pip uninstall pyrampl
# or
#!pip uninstall pyrampl

Requirement already satisfied: pyrampl in d:\python\my_pkgs\pyrampl (1.3)
Note: you may need to restart the kernel to use updated packages.

• After installation, you may need to restart this notebook.

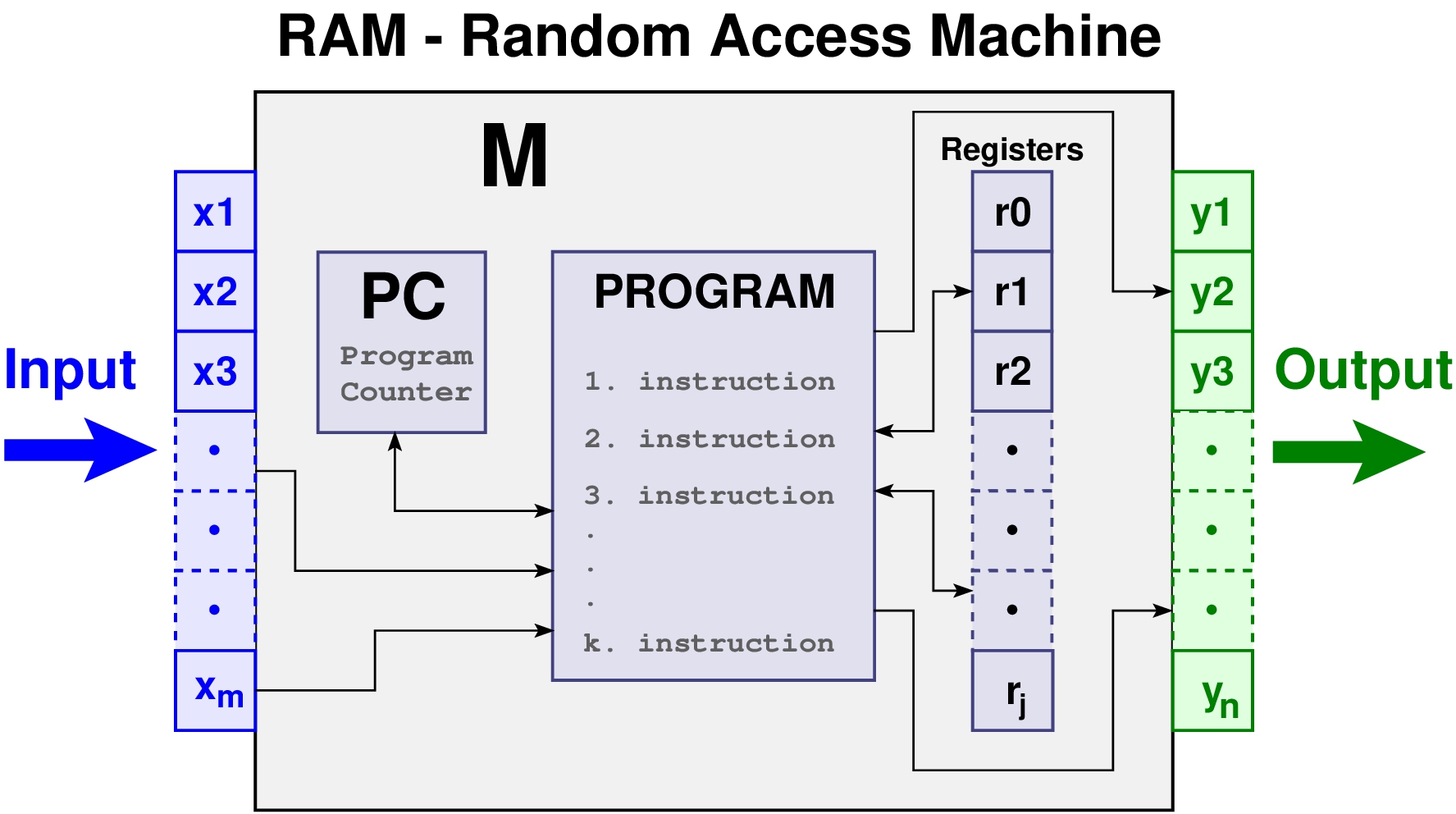
Introduction

• PyRamPL is a simple Python package for simulating Random Access Memory Machine programs within the context of an introductory course on computational models.
• It is a lightweight package especially designed for small RAM programs, such as those that are presented in introductory academic courses on the theory of computation.
• It can be a useful companion for theoretical courses on computation models and languages who wish also to engage the students with some programming experience and skills.
  • It was designed to be used in such a course by the author (Hebrew book at http://samyzaf.com/afl.pdf).
  • It enables students to easily experiment with RAM programs for their exercises, and to test correctness of their solutions.
• It also provide an opportunity for students to get a taste of how programming looks like while learning theoretical computation course.
• There are many different definitions of a RAM machine in the literature but from an educational perspective most of them are adequate for presenting a computational model resembling a modern computer system and its associated assembly programming language.

• WARNING! Our current very early version of PyRamPL is not yet making good syntactical checks, so make sure to write your RAM programs correctly or else you will not get any meaningful feedback! Since RAM programs have a very simple syntax we do not expect this to be a real problem.

  

RAM machine program syntax

Instruction	Description
$a=b$	Load register $b$ to register $a$
$a=i$	Load integer $i$ to register $a$
$a = b+c$	Add $b$ and $c$ and store the result in $a$
$a=b-c$	Subtraction
$a = b * c$	Multiplication
JUMP(i)	Jump to instruction i (PC = i)
JZERO(r, i)	If $r=0$ jump to instruction i
JPOS(r, i)	If $r>0$ jump to instruction i
JE(a, b, i)	If $a=b$ jump to instruction i
HALT	Stop the program

</font>

Example1: DIVMOD program

The following RAM program computes the integer quotient and a remainder ($y_1$ and $y_2$) after dividing $x_1$ by $x_2$

PROGRAM DIVMOD(x1, x2 : y1, y2)
    1. r1 = x1
    2. r2 = x2
    3. r0 = r2 - r1
    4. JPOS(r0, 8)
    5. r3 = r3 + 1
    6. r1 = r1 - r2
    7. JUMP(3)
    8. y1 = r3
    9. y2 = r1
    10. HALT

• The common practice is to build a Flow Diagram for your algorithm before you actually write the RAM program.
• In the following flow diagram for DIVMOD we have also added instruction labels that correspond to the RAM code (these are normally not part of a flow diagram) to make it easier to comprehend the RAM program.

Loading the PyRamPL package

• After installing the PyRamPl package, you need to import it.
• The following command imports PyRamPl to your Python interpreter.
• We have also imported a few IPython display utilities for displaying Markdown and LaTeX tables.

from pyrampl import *
from IPython.display import display, Markdown, Latex

code = """
PROGRAM DIVMOD(x1, x2 : y1, y2)
    1. r1 = x1
    2. r2 = x2
    3. r0 = r2 - r1
    4. JPOS(r0, 8)
    5. r3 = r3 + 1
    6. r1 = r1 - r2
    7. JUMP(3)
    8. y1 = r3
    9. y2 = r1
    10. HALT
"""

DIVMOD = Ram("DIVMOD", code)

y1, y2 = DIVMOD(17,5)
print(f"Dividing 17 by 5 result: y1={y1}, y2={y2}")

Dividing 17 by 5 result: y1=3, y2=2

• Note that we first define our RAM program as text string code, and then create a Ram object by invoking the Ram Python class.
• The Ram class accepts two arguments:
  • Machine name
  • Program text or file name for the program text
• If we put our program text in a file like divmod.ram, we can also create our machine object with a command such as

  DIVMOD = Ram("DIVMOD", "divmod.ram")

• In all examples we use capital letter names for the Ram objects. Usually identical to their internal names.

Example 2: EXP - building RAM machine for the exponent operation

• As we already have addition and multiplication in our base RAM instructions, we now show how to build a RAM machine for the exponential function.
• Lets first start with a flow diagram for the exponential function

code = """
PROGRAM EXP(x1, x2 : y1, y2)
    1. r1 = x1
    2. r2 = x2
    3. JZERO(r1, 9)
    4. r3 = 1
    5. JZERO(r2, 14)
    6. r3 = r3 * r1
    7. r2 = r2 - 1
    8. JUMP(5)
    9. JZERO(r2, 12)
    10. y1 = 0
    11. JUMP(15)
    12. y2 = 1
    13. JUMP(15)
    14. y1 = r3
    15. HALT
"""

• As you can see, our EXP version has two outputs $y_1$ and $y_2$
• The first one holds the exponential result if the input is legal.
• In case of an illegal input like $x_1=x_2=0$, the second output will be set to $y_2=1$

EXP = Ram("EXP", code)

y1,y2 = EXP(2,5)
print(f"y1={y1}, y2={y2}")

y1=32, y2=0

y1,y2 = EXP(0,0)
print(f"y1={y1}, y2={y2}")

y1=0, y2=1

Example 3: PRIME - checking if an integer is a prime number

• Once we have built a RAM machine such as DIVMOD, we can use it as an instruction within a new RAM machine.
• Formally, a RAM machine which used other RAM machine is called Generalized RAM Machine, but there is a Theorem that assures that for every generalized RAM machine there is an equivalent RAM machine
• The following flow diagram for the PRIME algorithm is using the DIVMOD instruction which we have defined above.

code = """
PROGRAM PRIME(x1 : y1)
    1. y1 = 1
    2. r1 = x1 - 3
    3. JPOS(r1, 5)
    4. HALT
    5. r0 = 2
    6. r1,r2 = DIVMOD(x1,r0)
    7. JZERO(r2, 11)
    8. r0 = r0 + 1
    9. JE(r0, x1, 12)
    10. JUMP(6)
    11. y1 = 0
    12. HALT
"""

PRIME = Ram("PRIME", code)
y = PRIME(19)
print(f"y={y}")

y=1

Computation Tables

• A simple way to observe and comprehend a RAM machine is by looking at snapshots of its register values.
• A snapshot consists of all the current values of input, memory, and output registers.
• A computation table consists of the full sequence of all the machine snapshots from its start to end.
• The PyRamPL package contains a special method for displaying this table as a markdown table (so you need to run it inside a markdown viewer such as an Ipython Jupyter Notebook)
• I the following example we display the computation table of the RAM machine PRIME for the input $x_1=7$.

display_table(PRIME, 7)

Frame	Instruction	x1	r0	r1	r2	y1
0	Init	7	0	0	0	0
1	1. y1 = 1	7	0	0	0	1
2	2. r1 = x1 - 3	7	0	4	0	1
3	3. JPOS(r1, 5)	7	0	4	0	1
4	5. r0 = 2	7	2	4	0	1
5	6. r1,r2 = DIVMOD(x1,r0)	7	2	3	1	1
6	7. JZERO(r2, 11)	7	2	3	1	1
7	8. r0 = r0 + 1	7	3	3	1	1
8	9. JE(r0, x1, 12)	7	3	3	1	1
9	10. JUMP(6)	7	3	3	1	1
10	6. r1,r2 = DIVMOD(x1,r0)	7	3	2	1	1
11	7. JZERO(r2, 11)	7	3	2	1	1
12	8. r0 = r0 + 1	7	4	2	1	1
13	9. JE(r0, x1, 12)	7	4	2	1	1
14	10. JUMP(6)	7	4	2	1	1
15	6. r1,r2 = DIVMOD(x1,r0)	7	4	1	3	1
16	7. JZERO(r2, 11)	7	4	1	3	1
17	8. r0 = r0 + 1	7	5	1	3	1
18	9. JE(r0, x1, 12)	7	5	1	3	1
19	10. JUMP(6)	7	5	1	3	1
20	6. r1,r2 = DIVMOD(x1,r0)	7	5	1	2	1
21	7. JZERO(r2, 11)	7	5	1	2	1
22	8. r0 = r0 + 1	7	6	1	2	1
23	9. JE(r0, x1, 12)	7	6	1	2	1
24	10. JUMP(6)	7	6	1	2	1
25	6. r1,r2 = DIVMOD(x1,r0)	7	6	1	1	1
26	7. JZERO(r2, 11)	7	6	1	1	1
27	8. r0 = r0 + 1	7	7	1	1	1
28	9. JE(r0, x1, 12)	7	7	1	1	1
29	12. HALT	7	7	1	1	1

display_table(EXP, 5, 2)

Frame	Instruction	x1	x2	r1	r2	r3	y1	y2
0	Init	5	2	0	0	0	0	0
1	1. r1 = x1	5	2	5	0	0	0	0
2	2. r2 = x2	5	2	5	2	0	0	0
3	3. JZERO(r1, 9)	5	2	5	2	0	0	0
4	4. r3 = 1	5	2	5	2	1	0	0
5	5. JZERO(r2, 14)	5	2	5	2	1	0	0
6	6. r3 = r3 * r1	5	2	5	2	5	0	0
7	7. r2 = r2 - 1	5	2	5	1	5	0	0
8	8. JUMP(5)	5	2	5	1	5	0	0
9	5. JZERO(r2, 14)	5	2	5	1	5	0	0
10	6. r3 = r3 * r1	5	2	5	1	25	0	0
11	7. r2 = r2 - 1	5	2	5	0	25	0	0
12	8. JUMP(5)	5	2	5	0	25	0	0
13	5. JZERO(r2, 14)	5	2	5	0	25	0	0
14	14. y1 = r3	5	2	5	0	25	25	0
15	15. HALT	5	2	5	0	25	25	0

display_table(DIVMOD, 18, 5)

Frame	Instruction	x1	x2	r0	r1	r2	r3	y1	y2
0	Init	18	5	0	0	0	0	0	0
1	1. r1 = x1	18	5	0	18	0	0	0	0
2	2. r2 = x2	18	5	0	18	5	0	0	0
3	3. r0 = r2 - r1	18	5	-13	18	5	0	0	0
4	4. JPOS(r0, 8)	18	5	-13	18	5	0	0	0
5	5. r3 = r3 + 1	18	5	-13	18	5	1	0	0
6	6. r1 = r1 - r2	18	5	-13	13	5	1	0	0
7	7. JUMP(3)	18	5	-13	13	5	1	0	0
8	3. r0 = r2 - r1	18	5	-8	13	5	1	0	0
9	4. JPOS(r0, 8)	18	5	-8	13	5	1	0	0
10	5. r3 = r3 + 1	18	5	-8	13	5	2	0	0
11	6. r1 = r1 - r2	18	5	-8	8	5	2	0	0
12	7. JUMP(3)	18	5	-8	8	5	2	0	0
13	3. r0 = r2 - r1	18	5	-3	8	5	2	0	0
14	4. JPOS(r0, 8)	18	5	-3	8	5	2	0	0
15	5. r3 = r3 + 1	18	5	-3	8	5	3	0	0
16	6. r1 = r1 - r2	18	5	-3	3	5	3	0	0
17	7. JUMP(3)	18	5	-3	3	5	3	0	0
18	3. r0 = r2 - r1	18	5	2	3	5	3	0	0
19	4. JPOS(r0, 8)	18	5	2	3	5	3	0	0
20	8. y1 = r3	18	5	2	3	5	3	3	0
21	9. y2 = r1	18	5	2	3	5	3	3	3
22	10. HALT	18	5	2	3	5	3	3	3

Example 4: An algorithm for computing the Greatest Common Divisor - GCD

• The following RAM program shows how we can code Euclid's GCD algorithm within the limited bound of the RAP program syntax.
• Note that it uses the DIVMOD machine which we defined earlier in two different places (re rectangles)
• It is not fully complete, as it avoids checking zero division issues.

code = """
PROGRAM GCD(x1, x2 : y1)
    1. r1 = x1
    2. r2 = x2
    3. JZERO(r1, 11)
    4. JZERO(r2, 13)
    5. r0 = r1 - r2
    6. JPOS(r0, 15)
    7. r0 = r2 - r1
    8. JPOS(r0, 17)
    9. y1 = r1
    10. HALT
    11. y1 = r2
    12. HALT
    13. y1 = r1
    14. HALT
    15. r3, r1 = DIVMOD(r1, r2)
    16. JUMP(3)
    17. r3, r2 = DIVMOD(r2, r1)
    18. JUMP(4)
    19. HALT
"""

GCD = Ram("GCD", code)

y = GCD(72,54)
print(f"The greatest common divisor of 72 and 54 is {y}")

The greatest common divisor of 72 and 54 is 18

Example 5: MAX4 - An algorithm for finding the maximum of 4 numbers

code = """
PROGRAM MAX4(x1, x2, x3, x4 : y1)
    1. y1 = x1
    2. r0 = y1 - x2
    3. JPOS(r0,5)
    4. y1 = x2
    5. r0 = y1 - x3
    6. JPOS(r0,8)
    7. y1 = x3
    8. r0 = y1 - x4
    9. JPOS(r0,11)
    10. y1 = x4
    11. HALT
"""

MAX4 = Ram("MAX4", code)

MAX4(2, 26, 9, 4)

26

Example 6: GETBIT and SETBIT

• The GETBIT and SETBIT are important for simulating a Turing machine by a RAM machine.
• The Turing machine tape is represented by a binary string encoded as an integer number.
• The GETBIT functions extracts the binary bit of an integer at a given place.
• For example: $41 = 101001_2$.
• Therefore GETBIT(41,0) = 1, GETBIT(41,1) = 0, GETBIT(41,2) = 0, GETBIT(41,3) = 1, etc.
• The SETBIT function sets the bit of an integer at a given location.
• For example: SETBIT(41,2,1) = 45.

code1 = """
PROGRAM GETBIT(x1, x2 : y1)
    1. r1 = x1
    2. r2 = x2
    3. r1,r0 = DIVMOD(r1, 2)
    4. JZERO(r2, 7)
    5. r2 = r2 -1
    6. JUMP(3)
    7. y1 = r0
    8. HALT
"""

code2 = """
PROGRAM SETBIT(x1, x2, x3 : y1)
    1. r0 = GETBIT(x1, x2)
    2. JE(r0, x3, 9)
    3. r1,r2 = EXP(2, x2)
    4. JPOS(x3, 7)
    5. y1 = x1 - r1
    6. HALT
    7. y1 = x1 + r1
    8. HALT
    9. y1 = x1
    10. HALT
"""

GETBIT = Ram("GETBIT", code1)
SETBIT = Ram("SETBIT", code2)

y1 = SETBIT(41, 2, 1)
print(y1)

45

display_table(SETBIT,9, 2, 1)

Frame	Instruction	x1	x2	x3	r0	r1	r2	y1
0	Init	9	2	1	0	0	0	0
1	1. r0 = GETBIT(x1, x2)	9	2	1	0	0	0	0
2	2. JE(r0, x3, 9)	9	2	1	0	0	0	0
3	3. r1,r2 = EXP(2, x2)	9	2	1	0	4	0	0
4	4. JPOS(x3, 7)	9	2	1	0	4	0	0
5	7. y1 = x1 + r1	9	2	1	0	4	0	13
6	8. HALT	9	2	1	0	4	0	13

Advanced topics

• This section is relevant for students with Python programming experience.
• We present few examples on how you can perform more thorough tests on your RAM programs
• Notes:
  • ic stands for the instruction counter
  • vardict stands for the variables dictionary (input/memory/output)

DIVMOD.init(17,5)
DIVMOD.run()
frames = DIVMOD.frames
for ic,instruction,vardict in frames:
    y1 = vardict['y1']
    y2 = vardict['y2']
    print(f"{ic:<5} {instruction:<20} y1={y1}   y2={y2}")

0     Init                 y1=0   y2=0
1     1. r1 = x1           y1=0   y2=0
2     2. r2 = x2           y1=0   y2=0
3     3. r0 = r2 - r1      y1=0   y2=0
4     4. JPOS(r0, 8)       y1=0   y2=0
5     5. r3 = r3 + 1       y1=0   y2=0
6     6. r1 = r1 - r2      y1=0   y2=0
7     7. JUMP(3)           y1=0   y2=0
8     3. r0 = r2 - r1      y1=0   y2=0
9     4. JPOS(r0, 8)       y1=0   y2=0
10    5. r3 = r3 + 1       y1=0   y2=0
11    6. r1 = r1 - r2      y1=0   y2=0
12    7. JUMP(3)           y1=0   y2=0
13    3. r0 = r2 - r1      y1=0   y2=0
14    4. JPOS(r0, 8)       y1=0   y2=0
15    5. r3 = r3 + 1       y1=0   y2=0
16    6. r1 = r1 - r2      y1=0   y2=0
17    7. JUMP(3)           y1=0   y2=0
18    3. r0 = r2 - r1      y1=0   y2=0
19    4. JPOS(r0, 8)       y1=0   y2=0
20    8. y1 = r3           y1=3   y2=0
21    9. y2 = r1           y1=3   y2=2
22    10. HALT             y1=3   y2=2

• You may isolate one or more registers and watch its progress

for ic,instruction,vardict in frames:
    r0 = vardict['r0']
    r1 = vardict['r1']
    r2 = vardict['r2']
    r3 = vardict['r3']
    print(f"ic={ic:<4} : {instruction:<16} : r0 ={r0:<3} : r1 = {r1:<3} : r2 = {r2:<3} : r3 = {r3:<3}")

ic=0    : Init             : r0 =0   : r1 = 0   : r2 = 0   : r3 = 0  
ic=1    : 1. r1 = x1       : r0 =0   : r1 = 17  : r2 = 0   : r3 = 0  
ic=2    : 2. r2 = x2       : r0 =0   : r1 = 17  : r2 = 5   : r3 = 0  
ic=3    : 3. r0 = r2 - r1  : r0 =-12 : r1 = 17  : r2 = 5   : r3 = 0  
ic=4    : 4. JPOS(r0, 8)   : r0 =-12 : r1 = 17  : r2 = 5   : r3 = 0  
ic=5    : 5. r3 = r3 + 1   : r0 =-12 : r1 = 17  : r2 = 5   : r3 = 1  
ic=6    : 6. r1 = r1 - r2  : r0 =-12 : r1 = 12  : r2 = 5   : r3 = 1  
ic=7    : 7. JUMP(3)       : r0 =-12 : r1 = 12  : r2 = 5   : r3 = 1  
ic=8    : 3. r0 = r2 - r1  : r0 =-7  : r1 = 12  : r2 = 5   : r3 = 1  
ic=9    : 4. JPOS(r0, 8)   : r0 =-7  : r1 = 12  : r2 = 5   : r3 = 1  
ic=10   : 5. r3 = r3 + 1   : r0 =-7  : r1 = 12  : r2 = 5   : r3 = 2  
ic=11   : 6. r1 = r1 - r2  : r0 =-7  : r1 = 7   : r2 = 5   : r3 = 2  
ic=12   : 7. JUMP(3)       : r0 =-7  : r1 = 7   : r2 = 5   : r3 = 2  
ic=13   : 3. r0 = r2 - r1  : r0 =-2  : r1 = 7   : r2 = 5   : r3 = 2  
ic=14   : 4. JPOS(r0, 8)   : r0 =-2  : r1 = 7   : r2 = 5   : r3 = 2  
ic=15   : 5. r3 = r3 + 1   : r0 =-2  : r1 = 7   : r2 = 5   : r3 = 3  
ic=16   : 6. r1 = r1 - r2  : r0 =-2  : r1 = 2   : r2 = 5   : r3 = 3  
ic=17   : 7. JUMP(3)       : r0 =-2  : r1 = 2   : r2 = 5   : r3 = 3  
ic=18   : 3. r0 = r2 - r1  : r0 =3   : r1 = 2   : r2 = 5   : r3 = 3  
ic=19   : 4. JPOS(r0, 8)   : r0 =3   : r1 = 2   : r2 = 5   : r3 = 3  
ic=20   : 8. y1 = r3       : r0 =3   : r1 = 2   : r2 = 5   : r3 = 3  
ic=21   : 9. y2 = r1       : r0 =3   : r1 = 2   : r2 = 5   : r3 = 3  
ic=22   : 10. HALT         : r0 =3   : r1 = 2   : r2 = 5   : r3 = 3